Identidades trigonometricas
Identidades reciprocas:
Existen 3 funciones trigonometricas fundamentales, Sen, Cos, Tan las reciprocas son Csc, Sec, Cot:
se les dice asi por que:
lunes, 6 de mayo de 2013
Funciones con razones trigonometricas
Funciones con razones trigonometricas
A partir dela siguiente expresion puede obtener el resultado alicando el valor de cada funcion
4Sen 3O° + 2Cos 6O° - 5Sen 45° + 3Tan 6O°=
4(O.5)+2(O.5)-5 (O.7O7)+ 3 (1.75)=
=4.6
tambien se puede resolver teniendo x.
A partir dela siguiente expresion puede obtener el resultado alicando el valor de cada funcion
4Sen 3O° + 2Cos 6O° - 5Sen 45° + 3Tan 6O°=
4(O.5)+2(O.5)-5 (O.7O7)+ 3 (1.75)=
=4.6
tambien se puede resolver teniendo x.
Funciones trigonometricas (continuacion)
Funciones trigonometricas
A partir de 2 datos podemos obtener todas las funciones trigonometricas correspondientes al triangulo rectangulo.
Obtener los elementos del triangulo si conocemos el valor de solo 2 de sus lados:
A partir de 2 datos podemos obtener todas las funciones trigonometricas correspondientes al triangulo rectangulo.
Obtener los elementos del triangulo si conocemos el valor de solo 2 de sus lados:
De radianes a grados
Un radian es la medida del angulo creado cuando envuelves el radio de un circulo alrededor de la circunferencia
1. Ecuacion para convertir radianes a grados Rx(180/PI)= G
(R es radianes y G es grados)
2. Poner la medida de tu angulo en radianes en la ecuacion anterior en el lugar de la R
3. Despues agrega las unidades a la respuesta final.
Es muy importante que pongas las respuestas en las unidades posibles, la respuesta fnal es que un angulo mide 2 radianes mediran 114.592°
Para convertir de grados a radianes:
1. Ecuacion para convertir radianes a grados Rx(180/PI)= G
(R es radianes y G es grados)
2. Poner la medida de tu angulo en radianes en la ecuacion anterior en el lugar de la R
3. Despues agrega las unidades a la respuesta final.
Es muy importante que pongas las respuestas en las unidades posibles, la respuesta fnal es que un angulo mide 2 radianes mediran 114.592°
Para convertir de grados a radianes:
PI(numero de grados)/180
Para convertir de radianes a grados:
180°(numero de radianes)/PI
Funciones trigonometricas
Las funciones trigonometricas de un triangulo rectangulo se obtienen a partir de un angulo dado y son las sigueintes:
Volumen
VOLÚMENES
Cubo: 1 a la tercera potencia (el volumen de un cubo se obtiene elevando al cubo la longitud de su arista
Prisma: ab x h (el volumen de un prisma se obtiene multiplicando la superficie de su base y después por altura del prisma)
Pirámide: (AB) x h / 3 ( el volumen de una pirámide es equivalente a un tercio del volumen de un prisma de igual base y altura)
Cilindro: (PIxr*) x h. (Se obtiene multiplicando la superficie de la base por altura del cilindro
Cono: (PIxr*)h / 3. (El volumen de un cono es equivalente a un tercio del volumen de un cilindro de igual base y altura.
Esfera: 3/4 x PI x r*
El volumen de una esfera es igual a 3/4 de PI por el radio al cubo.
EJERCICIOS:
Una pecera mide 1.5m de largo, 1m de ancho y O.8Om de altura. Si a una jarra le caben O.OO2 m3 de agua ¿Se puede llenar la pecera con 2O jarras de agua?
Solución:
Primero se debe sacar el volumen de la pecera (1.5x1xO.8O= 1.2)
Se hace una regla de tres
si a una jarra le caben O.OO2 a 2O jarras cuanto le caben = O.4 m3
Respuesta: con 2O jarras no se podria llenar la pecera por que tiene O.4 y la pecera necesita 1.2.
Una piramide de Egipto mide 230m de lado y 153 m de alto ¿que volumen tiene si su base es cuadrada?
Solucion: Si su base es cuadrada se aplica primero la formula para sacar el area de la base
23Ox23O=52900 despues se multiplica por la altura que es por 153 da un total de 8O937OO luego se divide entre tres ya que es una piramide y el resultado es de °°° 2697900m al cubo
Cubo: 1 a la tercera potencia (el volumen de un cubo se obtiene elevando al cubo la longitud de su arista
Prisma: ab x h (el volumen de un prisma se obtiene multiplicando la superficie de su base y después por altura del prisma)
Pirámide: (AB) x h / 3 ( el volumen de una pirámide es equivalente a un tercio del volumen de un prisma de igual base y altura)
Cilindro: (PIxr*) x h. (Se obtiene multiplicando la superficie de la base por altura del cilindro
Cono: (PIxr*)h / 3. (El volumen de un cono es equivalente a un tercio del volumen de un cilindro de igual base y altura.
Esfera: 3/4 x PI x r*
El volumen de una esfera es igual a 3/4 de PI por el radio al cubo.
EJERCICIOS:
Una pecera mide 1.5m de largo, 1m de ancho y O.8Om de altura. Si a una jarra le caben O.OO2 m3 de agua ¿Se puede llenar la pecera con 2O jarras de agua?
Solución:
Primero se debe sacar el volumen de la pecera (1.5x1xO.8O= 1.2)
Se hace una regla de tres
si a una jarra le caben O.OO2 a 2O jarras cuanto le caben = O.4 m3
Respuesta: con 2O jarras no se podria llenar la pecera por que tiene O.4 y la pecera necesita 1.2.
Una piramide de Egipto mide 230m de lado y 153 m de alto ¿que volumen tiene si su base es cuadrada?
Solucion: Si su base es cuadrada se aplica primero la formula para sacar el area de la base
23Ox23O=52900 despues se multiplica por la altura que es por 153 da un total de 8O937OO luego se divide entre tres ya que es una piramide y el resultado es de °°° 2697900m al cubo
Área
ÁREA
El área de una figura es la medida de la superficie y medir una superficie es determinar cuantas veces contiene a otra superficie coincida.
El área de un polígono regular es igual al perímetro por apotema sobre dos.
Para los polígonos irregulares debemos dividir entre triángulos y rectángulos y sumar cada área.
Ejercicios:
 La glorieta del ángel mide 18m de radio, se circula con una malla de alambre ¿cuantos metros se utilizarán?
La glorieta del ángel mide 18m de radio, se circula con una malla de alambre ¿cuantos metros se utilizarán?*solucion: se debe de aplicar la fórmula para sacar el perímetro del círculo la cual es:
P= PI X diámetro
P= 3.1416x36
P=113.097m
Un espejo mide 1.25m de diámetro ¿qué área tiene?
Para sacar el área de un círculo se debe aplicar la fórmula de A= PIxr* (lo usamos como al cuadrado)
Se sustituye la fórmula:
A=3.1416x0.625*
A=3.1416x0.390
A=1.22m*
Perímetro
Áreas, volúmenes y perímetro
Perímetro de un polígono regular:
Un polígono es una figura delimitada por lados, cuando esos lados son iguales y todos los ángulos internos también miden lo mismo entonces el polígono se llama REGULAR
El perímetro de un polígono es la suma de longitud de cada lado, si el polígono es regular, entonces el perímetro es igual al número de lados por la longitud de uno de ellos.
P= (# lados) (longitud)
Ejercicios:
Calcula el perímetro de un terreno cuadrado si cada lado mide 5 m.
Solución:
Se suman los lados del terreno cuadrado (siempre hay que fijarse que forma nos piden) así como aplicando la fórmula
P= 4lados por 5 = 20m
Cual es el perímetro de un terreno pentágonal si sus lados miden 13m
P= (5 lados)(13)= 65m
Calcula el perímetro de un decágono si sus lados miden 25 m
P= (10 lados) (25)= 250m
Si el perímetro de un triángulo equilátero es de 99m ¿cuanto mide cada lado?
Solución:
Se debe de divir los 99 m entre tres para sacar el de cada lado = 33m
Determina el perímetro de un octágono de 39 cm por lado
P= (8 lados)(39)= 312cm
Perímetro de un polígono regular:
Un polígono es una figura delimitada por lados, cuando esos lados son iguales y todos los ángulos internos también miden lo mismo entonces el polígono se llama REGULAR
El perímetro de un polígono es la suma de longitud de cada lado, si el polígono es regular, entonces el perímetro es igual al número de lados por la longitud de uno de ellos.
P= (# lados) (longitud)
Ejercicios:
Calcula el perímetro de un terreno cuadrado si cada lado mide 5 m.
Solución:
Se suman los lados del terreno cuadrado (siempre hay que fijarse que forma nos piden) así como aplicando la fórmula
P= 4lados por 5 = 20m
Cual es el perímetro de un terreno pentágonal si sus lados miden 13m
P= (5 lados)(13)= 65m
Calcula el perímetro de un decágono si sus lados miden 25 m
P= (10 lados) (25)= 250m
Si el perímetro de un triángulo equilátero es de 99m ¿cuanto mide cada lado?
Solución:
Se debe de divir los 99 m entre tres para sacar el de cada lado = 33m
Determina el perímetro de un octágono de 39 cm por lado
P= (8 lados)(39)= 312cm
Teorema de PITAGORAS
TEOREMA DE PITAGORAS
La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa
Este teorema se utiliza en los triángulos rectángulos
Para verificar que un triángulo es rectángulo podemos aplicar también el teorema de PITAGORAS ejercicios:
Indica sí los siguientes triángulos son rectángulos:
A) 4, 7.5 y 8.5
Solucion: 7.5"+4"= 8.5"
56.25+16= 72.25 °°° Si es un triángulo rectángulo °°°
72.25= 72.25
* siempre la cantidad más grande será la HIPOTENUSA
B) 61, 60 y 13
Solución: 60"+13"=61"
3600+169=3721
3769 /=/ 3721 °°° No es un triángulo rectángulo °°°
Cualquier triángulo se puede convertir en triángulo rectángulo para obtener sus medidas por ejemplo:
-En un triángulo isósceles se desea conocer la altura y conocemos que la base es de 16 y los lados iguales a 10
La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa
Este teorema se utiliza en los triángulos rectángulos
Para verificar que un triángulo es rectángulo podemos aplicar también el teorema de PITAGORAS ejercicios:
Indica sí los siguientes triángulos son rectángulos:
A) 4, 7.5 y 8.5
Solucion: 7.5"+4"= 8.5"
56.25+16= 72.25 °°° Si es un triángulo rectángulo °°°
72.25= 72.25
* siempre la cantidad más grande será la HIPOTENUSA
B) 61, 60 y 13
Solución: 60"+13"=61"
3600+169=3721
3769 /=/ 3721 °°° No es un triángulo rectángulo °°°
Cualquier triángulo se puede convertir en triángulo rectángulo para obtener sus medidas por ejemplo:
-En un triángulo isósceles se desea conocer la altura y conocemos que la base es de 16 y los lados iguales a 10
Ángulos internos de un polígono
Ángulos internos de un polígono
Los ángulos internos de un polígono se obtienen dividiendo ese polígono en triángulo para ver cuantos se forman internamente por ejemplo:
Teoremas
TEOREMAS
Si tenemos dos ángulos complementarios congruentes con otros dos, entonces el complemento de este tambien será congruente
Si tenemos dos ángulos suplementarios congruentes con otros dos, entonces el suplementario de este también será congruente.
Si tenemos dos ángulos complementarios congruentes con otros dos, entonces el complemento de este tambien será congruente
Si tenemos dos ángulos suplementarios congruentes con otros dos, entonces el suplementario de este también será congruente.
EJERCICIO:
Congruencia
Triángulos congruentes:
Dos triángulos son congruentes si tienen el mismo tamaño y forma de tal manera que sí los superponemos uno con otro coinciden de manera exacta.

/\ ABC~/\ DEF
Vértice < Angulo Lados
A= D. < a=d. AB=DE
B=E. < b=e. BC=EF
C=F. < c=f. AC=DF
Sabemos que la suma de los tres ángulos internos de un triángulo es igual a 180* y también conocemos los tres postulados de congruencia en los triángulos:
ALA, LAL, LLL
EJERCICIO:
Dos triángulos son congruentes si tienen el mismo tamaño y forma de tal manera que sí los superponemos uno con otro coinciden de manera exacta.

/\ ABC~/\ DEF
Vértice < Angulo Lados
A= D. < a=d. AB=DE
B=E. < b=e. BC=EF
C=F. < c=f. AC=DF
Sabemos que la suma de los tres ángulos internos de un triángulo es igual a 180* y también conocemos los tres postulados de congruencia en los triángulos:
ALA, LAL, LLL
EJERCICIO:
Polígonos
POLÍGONOS
Los polígonos son figuras formadas por más de tres lados, los cuales forman su perímetro, existen polígonos irregulares los cuales son formados por lados de diferente longitud y los polígonos regulares que son formados por lados con la misma longitud.
Mencionare la construcción de un cuadrado,un octágono, un triángulo, hexágono y dodecágono a partir de un círculo cualquiera:
Para el cuadrado:
1.- Trazar un círculo de cualquier longitud
2.- Marcar su diámetro
3.- Trazar su mediatriz
4.- Unir los puntos de su diámetro y la mediatriz.
Para el octágono:
1.- Trazar un círculo
2.- Marcar su diámetro
3.- Trazar su mediatriz
4.- Trazar su bisectriz
5.- Unir los puntos
1.- Trazar un círculo
2.- Trazar la mediatriz
3.- Posado en A abre hasta O y trazar un medio círculo (puntos E,F)
4.- Unir los puntosB,E,F
1.- Trazar un círculo
2.- Trazar la mediatriz
3.- Pasarse en A y en B hasta abrir a O y marcar 2 medios
círculos (puntos E,F,G y H)
círculos (puntos E,F,G y H)
4.- Unir F,H,B,G,E,A
Para el dodecágono:
1.- Trazar un círculo
2.- Trazar la mediatriz
3.- Pasarse en A, B, C, D y abrir hasta O trazar un medio círculo en cada punto
4.- Unir todos los puntos
Rectas Importantes
RECTAS IMPORTANTES
Radio: el radio de una circunferencia es el segmento que une el centro dela circunferencia con un punto cualquiera de la misma.
Cuerda: La cuerda es un segmento que une dos puntos de la circunferencia.
Diámetro: Es un segmento que pasa por el centro y une dos puntos opuesto por la circunferencia.
Tangente: La tangente es una recta que toca de un punto a la circunferencia.
Secante: la secante es una recta que corta a una circunferencia en dos puntos.
jueves, 21 de marzo de 2013
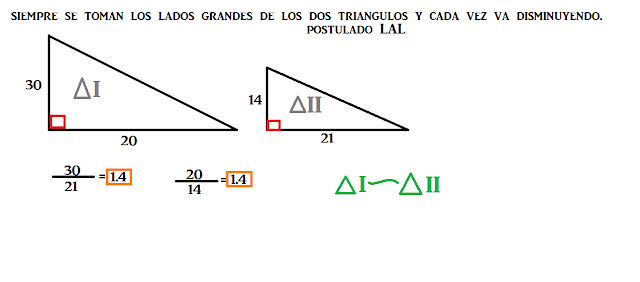
Semejanzas de triángulos
Semejanza de triángulos
Los triangulos son semejantes cuando tienen la misma forma aunque tengan diferente tamaño.
Dos triangulos son semejantes si sus angulos respectivos son congruentes y sus lados honologos y proporcionales.
Al comparar los lados orrespondientes de un triangulo con respecto al otro y los tres tienen la misma proporcionalidad se obtienen las relaciones.
lunes, 11 de marzo de 2013
Desigualdad de los triángulos
Postulado de la desigualdad: en todo triángulo la suma de dos de sus lados cualquiera debe ser mayor a la medida al lado restante.
A) 4,5,17 .. Se hacen las combinaciones: 4+5=9<17. 5+17=22>4. 17+4= 21>5... No se puede ya que por el postulado de la desigualdad dice que dos de sus lados de cualquiera debe ser mayor a la medida del lado restante.
B) 4,5,7.. Se hacen las combinaciones 5+7=12>4. 5+4=9>7. 7+4=11>5. Se realiza y es un triángulo escaleno acutángulo.
A) 4,5,17 .. Se hacen las combinaciones: 4+5=9<17. 5+17=22>4. 17+4= 21>5... No se puede ya que por el postulado de la desigualdad dice que dos de sus lados de cualquiera debe ser mayor a la medida del lado restante.
B) 4,5,7.. Se hacen las combinaciones 5+7=12>4. 5+4=9>7. 7+4=11>5. Se realiza y es un triángulo escaleno acutángulo.
Ejercicios de triángulos.
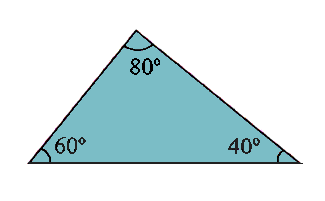
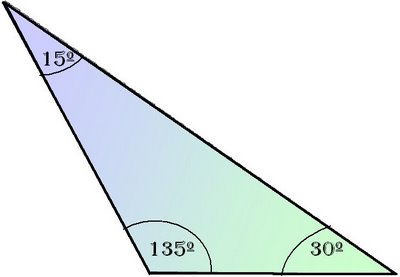
Si el triángulo está formado por los grados:
40*, 25* y 115*= obtusangulo
42*,48* y 90*= rectángulo.
60*,60* y 60*= esquíangulo
80*,45* y 55*= acutángulo.
Explica si el triángulo es isósceles o rectángulo ¿Por qué?
El triángulo tiene un ángulo de 90* y dos lados iguales: rectángulo ya que tiene un ángulo de 90* y también isósceles ya que tiene dos lados iguales.
40*, 25* y 115*= obtusangulo
42*,48* y 90*= rectángulo.
60*,60* y 60*= esquíangulo
80*,45* y 55*= acutángulo.
Explica si el triángulo es isósceles o rectángulo ¿Por qué?
El triángulo tiene un ángulo de 90* y dos lados iguales: rectángulo ya que tiene un ángulo de 90* y también isósceles ya que tiene dos lados iguales.
Triángulos
La suma de todos los ángulos internos nos debe de dar 180*
La suma de todos los ángulos externos nos debe de dar 360*
::::: ángulos formados por dos lados paralelos cortados por una secante:::::
Cuando dos rectas paralelas son cortadas por otra recta se formarán ocho ángulos relacionados...
Se debe de identificar si son agudos, obtusos o rectos, también se toma en cuenta que hay ángulos opuestos al vértice, ángulos suplementarios y los ángulos internos como externos.
La suma de todos los ángulos externos nos debe de dar 360*
::::: ángulos formados por dos lados paralelos cortados por una secante:::::
Cuando dos rectas paralelas son cortadas por otra recta se formarán ocho ángulos relacionados...
Se debe de identificar si son agudos, obtusos o rectos, también se toma en cuenta que hay ángulos opuestos al vértice, ángulos suplementarios y los ángulos internos como externos.
sábado, 16 de febrero de 2013
Clasificación de los triangulos segun sus lados
Clasificación de los triangulos segun sus lados:
Triangulo equilatero: Son los triangulos cuyos tres lados son iguales.
*nota: si los tres lados son iguales los angulos tambien seran iguales.
Triangulo isosceles: Tiene dos lados iguales y uno desigual.
*nota: en los lados iguales deben tener angulos iguales.
Triangulo escaleno: Este triangulo tiene todos sus lados diferentes.
*nota: todos sus lados diferentes asi que sus angulos son diferentes.
Triangulo equilatero: Son los triangulos cuyos tres lados son iguales.
*nota: si los tres lados son iguales los angulos tambien seran iguales.
Triangulo isosceles: Tiene dos lados iguales y uno desigual.
*nota: en los lados iguales deben tener angulos iguales.
Triangulo escaleno: Este triangulo tiene todos sus lados diferentes.
*nota: todos sus lados diferentes asi que sus angulos son diferentes.
Clasificacion de los triangulos por ángulos
Clasificacion de los triangulos segun sus ángulos:
Triangulo rectangulo: Tiene un angulo recto, en un triangulo rectangulo el lado opuesto al angulo recto se llama hipotenusa y los lados peroendiculares que forman en angulo recto ser llaman catetos.
Todo triangulo rectangulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Triangulo acutangulos: Si tienen tres ángulos agudos (menores a 90°)
Triangulo obtusángulo: Si tienen un ángulo obtuso (más de 9O°)
Triangulo rectangulo: Tiene un angulo recto, en un triangulo rectangulo el lado opuesto al angulo recto se llama hipotenusa y los lados peroendiculares que forman en angulo recto ser llaman catetos.
Todo triangulo rectangulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Triangulo acutangulos: Si tienen tres ángulos agudos (menores a 90°)
Triangulo obtusángulo: Si tienen un ángulo obtuso (más de 9O°)
Pequeño problema de ángulos
Problema de ángulos:
Si el ángulo A y el ángulo B son complementarios encuentra el valor de "x" de los ángulos A&B si ángulo A= 5x-4 y el ángulo B= 4x+9, los ángulos estan dado en grados.
solución: Se suman los ángulos A&B:
5x-4
4x+9 ° la suma de los dos es: 9x+5=90 {el resultado es noventa ya que es complementario y los complementarios llegan a noventa}
se realiza la funcion 9x+5=90:
9x=90-5
9x= 85
x= 85/9
x= 9.4
Ya con el resultado de la "x" podemos sustituir las funciones de los ángulos A&B.
A) 5(9.4)-4
47-4= 43°
B) 4(9.4)+9
38+9= 47° °°Los grados sumados dan 90° °°
Si el ángulo A y el ángulo B son complementarios encuentra el valor de "x" de los ángulos A&B si ángulo A= 5x-4 y el ángulo B= 4x+9, los ángulos estan dado en grados.
solución: Se suman los ángulos A&B:
5x-4
4x+9 ° la suma de los dos es: 9x+5=90 {el resultado es noventa ya que es complementario y los complementarios llegan a noventa}
se realiza la funcion 9x+5=90:
9x=90-5
9x= 85
x= 85/9
x= 9.4
Ya con el resultado de la "x" podemos sustituir las funciones de los ángulos A&B.
A) 5(9.4)-4
47-4= 43°
B) 4(9.4)+9
38+9= 47° °°Los grados sumados dan 90° °°
jueves, 14 de febrero de 2013
Ángulos:3
Ángulos:
Llano: el ángulo llano es el cual mide 180*
Recto: Un ángulo recto es el cual mide 90*
Agudo: un ángulo agudo es el que mide menos de 90*
Obtuso: un ángulo obtuso es el que mide más de 90*
Angulo adyacente: los ángulos adyacentes comparten el vértice y uno de sus lados
Angulo opuesto por el vértice: son los ángulos opuestos cuando se cruzan dos líneas y son iguales
Angulo suplementario: los ángulos son suplementarios si suman 180*
Angulo complementario: son aquellos ángulos cuyas medidas suman suman 90*
miércoles, 6 de febrero de 2013
Transformacion de una funcion estandar a una forma general
Transformacion de una funcion estandar a una forma general:
La funcion que realizaremos sera:
a= 4 (1,3)
el a= 4 h= 1 k= 3
Quedaria la funcion:
4(x-1)"+3= f(x)
Se realiza primero el binomio cuadrado:
4(x"-2x+1)+3= f(x)
Despues se realiza multipplicando el 4 por lo que esta adentro del parentesis:
4x"-8x+4+3= f(x)
se realiza y ese es el resultado final:
4x"-8x+7= f(x)
Cuando el coeficiente cuadratico es diferente a 1
Cuando el coeficiente cuadratico es diferente de 1:
La funcion sera:
La funcion sera:
2x"-12x+19
Primero se agrupan los terminos cuadraticos y lineales:
[2x"-12x]+19
Luego se debe dividir para que el 2x" quede en x" y el otro tambien se divide entre el 2 del x:
2[x"-6x]+19
Despues se obtiene b del termino lineal de todo lo que se encuentra dentro del corchete que es con la formula:
(b/2)"
Se sustituye la b, quedaria:
(-6/2)"= (-3)"= 9
Se suma y se resta el valor obtenido dentro de los corchetes:
2[x"-12x+9-9]+19
Se factoriza para tener el trinomio cuadrado perfecto:
2[x"-12x+9-9]+19
2[(x-3)"-9]+19
Se aplica jerarquia de operaciones:
2(x-3)"-18+19
2(x-3)"+1
a= 2 h=3 k= 1
Vetice(3,1)
Ahora para finalizar tabularemos:
X | Y
1 | 9
2 | 3
3 | 1
4 | 3
5 | 9
Y se hace la parabola:
miércoles, 30 de enero de 2013
Parabola:3
Metodo para acompletar un trinomio cuadrado perfecto:
Y= x"+4x+1
Se debe de separa en a,b y c, quedaria:
a= 1 b= 4 c= 1
Despues se aplica la formula:
Y= (b/2)"
Se sustituye:
Y= (4/2)" = 4
Queda cuatro ya que 4/2 da 2 y eso se eleva al cuadrado que seria 2x2= 4
Ahora se pone de nuevo la funcion original pero entre el 4x+1 se pone el cuatro de la formula y se le aumenta un -4 que quedaria asi:
x"+4x+4-4+1
Se saca la raiz de x" , despues el signo del segundo numero y la raíz del tercer número:
(x+2)"-3
El -3 es por que los dos ultimos numeros se realizaron
La formula que se utilizo fue Y= (x-h)"-k
h= -2
k= -3
El -2 salio por que en la funcion esta el +2 pero se realiza con el -h de la formula y como mas por menos da menos, salio el -2
El vertice esta en (-2,-3)
Tabularemos:
X | Y
O | 1
-1 | -2
-2 | -3
-3 | -2
-4 | 1
(O)"+4(O)+1= 1
(-1)"+4(-1)+1= -2
(-2)"+4(-2)+1= -3
(-3)"+4(-3)+1= -2
(-4)"+4(-4)+1= 1
Los elementos de la parabola:
Ramas: ARRIBA
Concavidad: POSITIVA
Vertice: (-2,-3)
Eje de simetria: (-2)
Minimo: (-3)
lunes, 28 de enero de 2013
Ecuaciones cadraticas en forma estandar
Ecuacion cuadratica en forma estandar
Y= a(x-h)"+k
Donde (a,h,k) segun sus valores la grafica se movera hacia arriba o abajo, a la derecha o a la izquierda y tambien se podra ensanchar o adelgazar.
Ahora pondremos en practica la forma estandar en:
Y= 3x"
a= 3 x=0 k=0
Sustituir y tabular
3(-3)"= 27
3(-2)"= 12
3(-1)"= 3
3(0)"= 0
3(1)"= 3
3(2)"= 12
3(3)"= 27
X | Y
-3 | 27
-2 | 12
-1 | 3
0 | 0
1 | 3
2 | 12
3 | 27
jueves, 24 de enero de 2013
Análisis del discriminante
Parábola
La función que se realizara pero con factorizacion será:
La función que se realizara pero con factorizacion será:
f(x)= -x" + 3x
Factorizada: (-x+3) (x+0)
-x+3=0 x+0=0
-x=-3 x=0
x= 3 x=0
Ya que tienes los dos puntos se realiza la la fórmula para saber donde queda el vértice sustituyendo los valores.
A= -1
B= 3
C= 0
Ahora se sustituyen las letras por números.
X=-3/2(-1)
X= -3/-2
X= 3/2
X= 1.5
Después ya que tenemos el punto X del vértice debemos sustituir las X en la función
F(x)= -(1.5)"+3(1.5)
-2.25+4.5= 2.25
F(x)= 2.25
miércoles, 23 de enero de 2013
Ejercicio de parabola
PARABOLA
(ejercicio)
La función que desarrollaremos es:
f(x)= x" + 2x - 3
(como lo mencionamos anteriormente que al cuadrado sera con las comillas (")
"Cuando el vertice esta fuera del origen para poder comenzar a tabular primero se obtiene el punto X del vertice, para obtener X se aplica la formula"
Para obtener los puntos se hace la formula general pero antes debemos sustituirlos:
a= 1
b= 2
c= -3
Y quedaria asi:
Se realiza y el resultado de la X seria:
X= -1
f(x)= x" + 2x -3
f(x)= (-1)"+ 2(-1) -3
f(x)= +1-2-3
f(x)= +1-5
f(x)= -4
Ahora ya tenemos los dos puntos de el vertice para la parabola pero para sacar los otros se debe de aplicar la formula general:
Las letras se sustituyen como lo hicimos arriba de a,b y c.
Y se hace la formula general (aqui lo haremos paso por paso)
Despues de sacar los puntos ahora tabularemos:
X | Y
-3 | O
-1 | -4
1 | O
La parabola quedaria asi:
Ramas: Arriba
Concavidad: positiva
Vertice (-1, -4)
eje de simetria (-1)
minimo (-4)
Suscribirse a:
Comentarios (Atom)