Clasificación de los triangulos segun sus lados:
Triangulo equilatero: Son los triangulos cuyos tres lados son iguales.
*nota: si los tres lados son iguales los angulos tambien seran iguales.
Triangulo isosceles: Tiene dos lados iguales y uno desigual.
*nota: en los lados iguales deben tener angulos iguales.
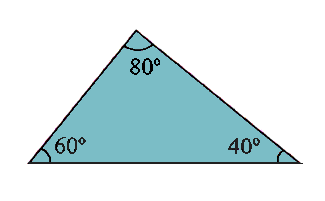
Triangulo escaleno: Este triangulo tiene todos sus lados diferentes.
*nota: todos sus lados diferentes asi que sus angulos son diferentes.
sábado, 16 de febrero de 2013
Clasificacion de los triangulos por ángulos
Clasificacion de los triangulos segun sus ángulos:
Triangulo rectangulo: Tiene un angulo recto, en un triangulo rectangulo el lado opuesto al angulo recto se llama hipotenusa y los lados peroendiculares que forman en angulo recto ser llaman catetos.
Todo triangulo rectangulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Triangulo acutangulos: Si tienen tres ángulos agudos (menores a 90°)
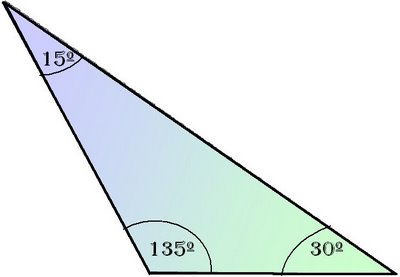
Triangulo obtusángulo: Si tienen un ángulo obtuso (más de 9O°)
Triangulo rectangulo: Tiene un angulo recto, en un triangulo rectangulo el lado opuesto al angulo recto se llama hipotenusa y los lados peroendiculares que forman en angulo recto ser llaman catetos.
Todo triangulo rectangulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Triangulo acutangulos: Si tienen tres ángulos agudos (menores a 90°)
Triangulo obtusángulo: Si tienen un ángulo obtuso (más de 9O°)
Pequeño problema de ángulos
Problema de ángulos:
Si el ángulo A y el ángulo B son complementarios encuentra el valor de "x" de los ángulos A&B si ángulo A= 5x-4 y el ángulo B= 4x+9, los ángulos estan dado en grados.
solución: Se suman los ángulos A&B:
5x-4
4x+9 ° la suma de los dos es: 9x+5=90 {el resultado es noventa ya que es complementario y los complementarios llegan a noventa}
se realiza la funcion 9x+5=90:
9x=90-5
9x= 85
x= 85/9
x= 9.4
Ya con el resultado de la "x" podemos sustituir las funciones de los ángulos A&B.
A) 5(9.4)-4
47-4= 43°
B) 4(9.4)+9
38+9= 47° °°Los grados sumados dan 90° °°
Si el ángulo A y el ángulo B son complementarios encuentra el valor de "x" de los ángulos A&B si ángulo A= 5x-4 y el ángulo B= 4x+9, los ángulos estan dado en grados.
solución: Se suman los ángulos A&B:
5x-4
4x+9 ° la suma de los dos es: 9x+5=90 {el resultado es noventa ya que es complementario y los complementarios llegan a noventa}
se realiza la funcion 9x+5=90:
9x=90-5
9x= 85
x= 85/9
x= 9.4
Ya con el resultado de la "x" podemos sustituir las funciones de los ángulos A&B.
A) 5(9.4)-4
47-4= 43°
B) 4(9.4)+9
38+9= 47° °°Los grados sumados dan 90° °°
jueves, 14 de febrero de 2013
Ángulos:3
Ángulos:
Llano: el ángulo llano es el cual mide 180*
Recto: Un ángulo recto es el cual mide 90*
Agudo: un ángulo agudo es el que mide menos de 90*
Obtuso: un ángulo obtuso es el que mide más de 90*
Angulo adyacente: los ángulos adyacentes comparten el vértice y uno de sus lados
Angulo opuesto por el vértice: son los ángulos opuestos cuando se cruzan dos líneas y son iguales
Angulo suplementario: los ángulos son suplementarios si suman 180*
Angulo complementario: son aquellos ángulos cuyas medidas suman suman 90*
miércoles, 6 de febrero de 2013
Transformacion de una funcion estandar a una forma general
Transformacion de una funcion estandar a una forma general:
La funcion que realizaremos sera:
a= 4 (1,3)
el a= 4 h= 1 k= 3
Quedaria la funcion:
4(x-1)"+3= f(x)
Se realiza primero el binomio cuadrado:
4(x"-2x+1)+3= f(x)
Despues se realiza multipplicando el 4 por lo que esta adentro del parentesis:
4x"-8x+4+3= f(x)
se realiza y ese es el resultado final:
4x"-8x+7= f(x)
Cuando el coeficiente cuadratico es diferente a 1
Cuando el coeficiente cuadratico es diferente de 1:
La funcion sera:
La funcion sera:
2x"-12x+19
Primero se agrupan los terminos cuadraticos y lineales:
[2x"-12x]+19
Luego se debe dividir para que el 2x" quede en x" y el otro tambien se divide entre el 2 del x:
2[x"-6x]+19
Despues se obtiene b del termino lineal de todo lo que se encuentra dentro del corchete que es con la formula:
(b/2)"
Se sustituye la b, quedaria:
(-6/2)"= (-3)"= 9
Se suma y se resta el valor obtenido dentro de los corchetes:
2[x"-12x+9-9]+19
Se factoriza para tener el trinomio cuadrado perfecto:
2[x"-12x+9-9]+19
2[(x-3)"-9]+19
Se aplica jerarquia de operaciones:
2(x-3)"-18+19
2(x-3)"+1
a= 2 h=3 k= 1
Vetice(3,1)
Ahora para finalizar tabularemos:
X | Y
1 | 9
2 | 3
3 | 1
4 | 3
5 | 9
Y se hace la parabola:
Suscribirse a:
Comentarios (Atom)